Se hace un mantenimiento preventivo periódico a motores de aviones, donde se debe cambiar un componente importante. La cantidad de motores programados para ese mantenimiento, durante los seis meses siguientes, se estima en 200, 180, 300, 198, 230 y 290 respectivamente. Todo el trabajo de mantenimiento se hace durante los dos primeros días del mes, cuando se puede cambiar un componente usado por uno nuevo, o por un componente reconstruido. La reconstrucción de los componentes usados se puede hacer en un taller local, y cuando salen están listos para usarse al principio del mes siguiente, o bien se pueden mandar a un taller central y en ese caso hay una espera de tres meses (que incluye al mes en que se hace el mantenimiento). El costo de reparación en el taller local es de $120 por componente. En el taller central el costo sólo es de $35 por componente. Un componente reconstruido que se usa en algún mes posterior causará un costo adicional de almacenamiento de $1.50 por unidad y por mes. Los componentes nuevos se pueden comprar a un costo de $200 cada uno, en el mes 1 y con 5% de aumento en el precio cada dos meses. Formular el problema, resolverlo utilizando algún paquete computacional.
Planteamos la tabla de transporte
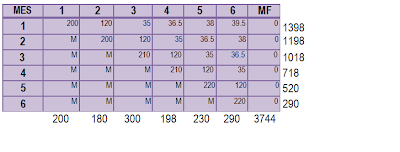
Aplicamos Vogel para encontar la solución básica
Aplicamos el método de multiplicadores para encontrar la variable de entrada
Como todos los valores de las variables son negativos, quiere decir que encontramos la solución optima que es:
Comparamos los resultados con los de un paquete computacional en esta caso WINQSB
Los resultados son iguales lo cual quiere decir que:
200 motores el mes 1 para el mes 1
200 motores el mes 1 para el mes 2
200 motores el mes 1 para el mes 3
200 motores el mes 2 para el mes 4
200 motores el mes 3 para el mes 5
200 motores el mes 4 para el mes 6
Con un costo de: $97 230.00





No hay comentarios:
Publicar un comentario